Linearizability testing S2 with deterministic simulation

With S2, it is a hard requirement that our Stream API operations exhibit linearizability. Linearizable systems are far simpler to reason about, and many applications are only possible to build on top of data platforms that offer strong consistency guarantees like this.

Because it's important, we also need to test it! We can gain confidence that S2 is linearizable by taking an empirical validation approach, using a model checker like Knossos, or Porcupine.

Last week I wired up a system for validating this property using S2 logs collected from our deterministic simulator. This post is a summary of that work.

Context

We’ve written a bit about our approach to testing S2 for correctness using deterministic simulation testing ("DST"). In short: we use turmoil to run the components of our distributed system — which, in production, are separate processes on different network hosts — within one, single threaded, Tokio runtime. The core of S2 is already in Rust, and we make use of Tokio, so turmoil is perfect (though we do have to mock external dependencies, like FoundationDB and S3).

Our setup provides both a deterministic environment for testing our system, as well as levers for injecting faults. We can run randomized workloads on it — which we do both as a CI step, and in much larger volumes in a nightly suite — and monitor for configurations (specific inputs, types of network stress, etc) that trigger violations of important invariants.

When an assertion is failed, we can easily recreate the exact steps which led to it just by restarting the simulation using the same seed.

It's hard to overstate how revolutionary this has been for our ability to build S2! At this point I can't imagine building infra without a DST framework.

While we assert on a lot of different conditions in our simulations, some correctness properties aren't feasible to evaluate during test runs as Rust assertions, and require additional tooling to verify after the fact.

Linearizability is an example of one such property — it’s a strong consistency model for distributed systems. If you aren’t familiar with it, a lot of great material has been written about what it entails. This post, by the author of the Porcupine checker, is a great place to start.

I’ll borrow from Martin Kleppmann’s summary in DDIA:

In a linearizable system, as soon as one client successfully completes a write, all clients reading from the database must be able to see the value just written. Maintaining the illusion of a single copy of the data means guaranteeing that the value read is the most recent, up-to-date value, and doesn’t come from a stale cache or replica. In other words, linearizability is a recency guarantee.

What to test

If you're not familiar with S2 (hello then, in that case!), the core data structure is the stream, which is an append-only log.

The API is very simple: you can append batches of records to the "tail" of a stream, read sequenced records starting at any position in the stream, and check-tail to see what the next assigned sequence number will be on the stream (i.e., the value of the "tail").

S2 Stream Operations

For an S2 stream to be linearizable, it just means:

(We also make strong consistency guarantees about S2's concurrency control mechanisms, like fencing tokens, but we’ll get back to that later.)

Verifying linearizability

We have a sense of what linearizability in S2 entails — how would we actually verify it?

I decided to try out Porcupine. It evaluates whether a client-observed log of concurrent calls to a system can be assembled into a total ordering in a way that satisfies linearizability.

Porcupine doesn’t test a live system directly, but rather evaluates a model of the system using a log collected from the real thing.

So first we need to represent S2 as a Porcupine model, then we need a way to collect relevant access logs from S2.

Modelling S2 in Porcupine

Linearizability validators are often demonstrated on "register" objects — key-value pairs essentially.

If you squint, an S2 stream can also be viewed as a type of register, where:

• Key = the name of the stream
• Value = a tuple of (tail, last_written_record)

For simplicity, we can store a hash of the last record, instead of the content itself.

To flesh this out a bit, we can see how the state of an actual S2 stream, and our associated register model, change in response to some successful append calls:

Stream State:                                    | Register State:
┌──────────────────────────────────────────────┐ │
│              Empty Stream                    │ │ (tail=0, content=0)
│                                              │ │
└──────────────────────────────────────────────┘ │
                         │                       │
                         ▼ append([a,b,c])       │
┌──────────────────────────────────────────────┐ │
│    seq:0    seq:1    seq:2                   │ │ (tail=3, content=hash(c))
│      a        b        c                     │ │
└──────────────────────────────────────────────┘ │
                         │                       │
                         ▼ append([d,e])         │
┌──────────────────────────────────────────────┐ │
│    seq:0    seq:1    seq:2    seq:3    seq:4 │ │ (tail=5, content=hash(e))
│      a        b        c        d        e   │ │
└──────────────────────────────────────────────┘ │
 

Since batches are appended atomically, we never expect to see intermediate states like (tail=4, content=hash(d)) — either the entire batch ([d,e]) would commit, or none of it does.

Step function

A model requires an initial state — for us, that’s just (tail=0, content=0) — and a step function which describes how to transform the register state, given an observed call input and output.

The model's step function signature looks like: step(current_state, observed_input, observed_output) → (is_legal, new_state). In other words, we need to provide a pure function that maps our prior register state, and the observed call/response, into a response indicating if a new state can legally be constructed — and if so, providing that resulting state.

The logic for the function depends on the input type (i.e., the type of call being made):

Note that only append will actually alter the register! Both read and check-tail will simply return the original current_state unchanged, unless an inconsistency is detected.

Porcupine uses this model to essentially solve for a linearizable sequence of transformations to our state — and will let us know if it’s impossible to do so.

Definite and indefinite failures

The model sketch above assumes that calls observed from S2 always succeed, but of course that’s not the case.

With calls that don’t cause side-effects, namely read and check-tail, failures are pretty simple to handle — we can simply change our model to reflect that an output’s tail or content values are optional, and won’t be provided if the call fails.

Appends are trickier, since they mutate the register. In S2, if an append call fails, we don’t necessarily know if the records became durable or not — and therefore, in our model, we don't know if we should update the tail and hash in the register or not.

Some failures may be definite, of course. For example, a validation error from S2, which tells us concretely that the batch was rejected; for these, we know there should be no change to the register.

But there's a wide class of indefinite failures for which we can’t know, just by looking at the output, if they took effect.

Porcupine lets us deal with this ambiguity via the NondeterministicModel type. Step functions in these models return a set of all possible state transformations, meaning that an append which receives an indefinite failure can, in our model, be witnessed as either producing an unchanged original state, or a state in which the batch was made durable and added to the tail. Both options can legally be part of a linearizable history.

An updated step function for indefinite failures would then look like this:

A linearizable history may pass through either one of these possibilities, but no others.

Is the model too basic?

In S2, a read needs to be capable of returning all prior acknowledged writes, not just the latest one. People aren’t using S2 as a KV store after all. Yet the model I’ve sketched above treats reads simply as a mechanism to receive the last record on the stream.

Our model would be more robust if the register value reflected the entire state of the stream, and each read returned that state.

When I originally thought about this, I decided that would be overkill, since S2 already contains many assertions around checksumming, and continuity of returned sequence numbers. These assertions in our code would halt and fail the DST even before we could collect a set of logs for Porcupine. But it’s true, this model could be made stronger by capturing the entire stream in the register.¹

Collecting concurrent histories

Porcupine can deal with either timed, or relative orderings for start/end events. To that end, I made a basic Rust library that performs a randomized workload on a single stream.

Rust is significant because it allows us to run the code within our internal turmoil-based DST — but anything could be used to collect these histories.

My code simply specifies a set of concurrent clients (Tokio tasks), which randomly alternate between read, check-tail, and append calls.

Any time a call starts or ends, the client emits a log event. These logs look like this:

{
  "event": {
    "Start": {
      "Append": {
        "num_records": 3,
        "last_record_xxh3": 375918985
      }
    }
  },
  "client_id": 19,
  "op_id": 6603
}

This is followed, some time later, with the corresponding op_id's return:

{
  "event": {
    "Finish": {
      "AppendSuccess": {
        "tail": 1683
      }
    }
  },
  "client_id": 19,
  "op_id": 6603
}

Model outputs

Our porcupine model can then try to assemble a linearizable history from our log. This even yields a neat visualization, where each step also displays the specific next possible states.

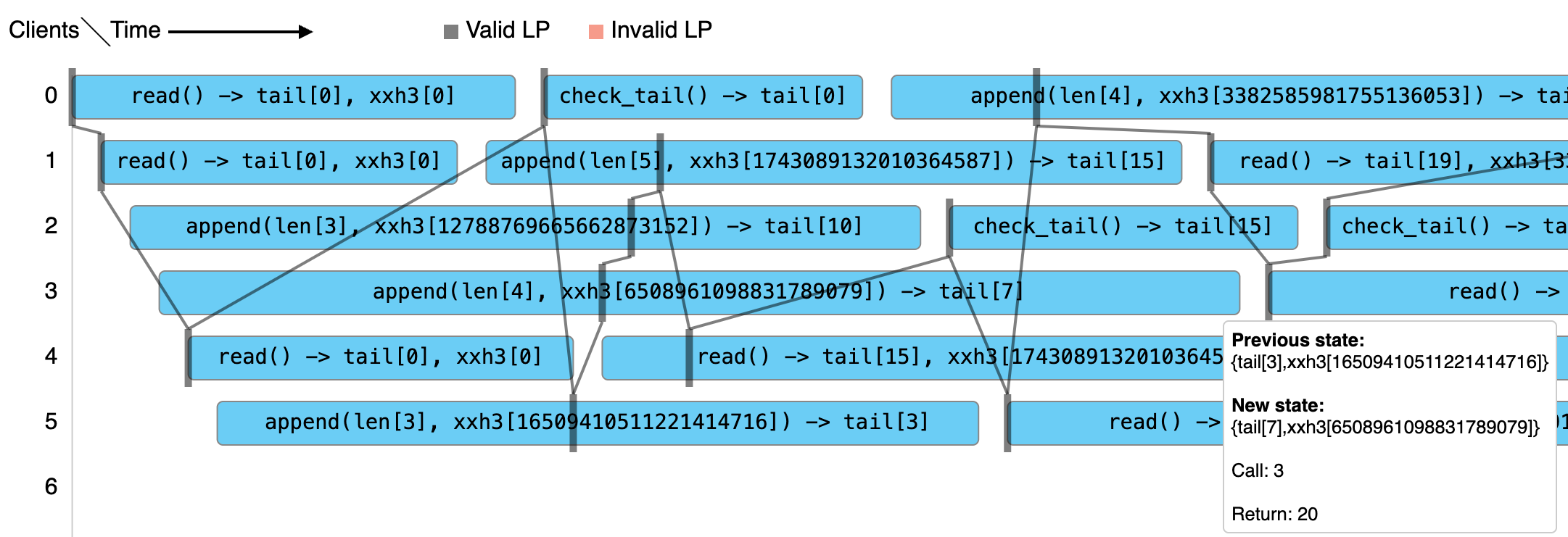Example of a Porcupine visualization. The line displays a valid linearizable sequencing of events through the observed histories of concurrent callers.

Deterministic simulation

At this point, we have the capability of collecting concurrent histories, and validating them for linearizability with a Porcupine model of S2. But, given this is an empirical test, we really want to be systematic in how we collect these histories.

For instance, it's important to validate that histories collected even when the system is under extreme stress are linearizable. Our DST allows us to do that, by giving us a platform for:

• Running parallel test invocations under different workload configurations
• Injecting network faults
• Causing component crashes or other loss of availability

And, thankfully, in a reproducible environment, where reusing the same seed lets us experience the same sequence of events.

Linearizability validation now happens as a step in our nightly suite.

Our sleek nightly test UI.

An interesting gotcha

When I first wired this up and actually started to run the Porcupine model in the context of our nightly suite, I discovered a number of trials which were reporting violations of linearizability. I started to see my professional life flashing across my eyes.

In reality, I was just discovering a flaw in my model, regarding how I was handling clients which experienced indefinite failures while appending — one which is probably familiar to followers of Jepsen content, but which I had failed to internalize and had to discover via the DST.

Recall that the concurrent clients used to collect logs for Porcupine will randomly switch between operations. In my initial setup, a client would continue making requests, even after experiencing an indefinite failure for an append (e.g., due to hitting a timeout). The client would simply report the indefinite failure, then move on to the next randomly selected operation — but this is unsafe!

Consider this sequence of events. For simplicity, assume there is only one concurrent client interacting with the system, and all operations are sequential:

This is totally possible to experience in my setup! In Step 3, it is true that the prior append had not become durable; but it is not true that it would not become so at a later moment. If we considered Step 2 to have ended with the indefinite failure, then this looks like a violation of linearizability.

How can this happen in the first place?

It’s possible that the prior indefinitely failed append was able to submit the batch to S2 before a network failure caused the client error — but S2 did receive it, it just hadn’t flushed it to object storage yet and thus made it durable.

Or alternatively, even if S2 had never received the batch at all, it’s possible that a prior append’s payload is caught in some network switch somewhere, indefinitely delayed, only to become unstuck in the future.

What to make of this

This isn’t actually a problem for linearizability of S2! The solution is just to consider any client that experiences an indefinite failure as essentially unsafe to continue using. In the history we feed to Porcupine, the end time of any indefinitely failed appends should be set to a moment after all other operations complete. This models the fact that these calls could still take effect on the register at any moment in the future. In a sense, the call can never be witnessed to have ended, because there is never a point at which we can definitively say it will no longer be possible to have an effect.

In a practical sense, if you are a user of S2, this might sound like a technicality: sure, it's linearizable — but if you experience a timeout, how do you actually proceed?

If you find yourself in this position, and need to know precisely if a failed append can or cannot become durable in the future, S2’s concurrency control mechanisms can achieve this.²

Additional steps

With pretty minimal tweaks to our model, we can also incorporate logic around our concurrency control mechanisms — i.e., that any append which specifies a match_seq_num (our version of a CAS essentially) must only succeed if the register’s tail matches the provided sequence number. We can also expand the register to include fencing tokens. Establishing a token via a fence record is a strongly consistent operation in S2, and by modeling that as part of the state we can be more confident that this is always the case.

In addition to our homegrown DST, we've also recently started experimenting with Antithesis's deterministic testing environment, and run this model as part of the workloads sent there. More about our experience with Antithesis soon!

If you're interested in the Porcupine model, check out the code on GitHub!